Existen muchas situaciones en las que queremos cambiar la trayectoria de un vehículo espacial. Por ejemplo para poner a un satélite en una órbita geoestacionaria debemos hacer varias maniobras por separado desde el lanzamiento hasta su puesta en órbita final. En otras ocasiones nos interesa sacar de órbita a un satélite que hemos dado de baja para hacerlo que reingrese a la tierra y se destruya. Hay otras maniobras más complicadas, como por ejemplo, el enviar una sonda a la luna, un vehículo a que orbite Marte o a cualquier otro cuerpo celeste, como la reciente misión Rosetta que envió la Agencia Espacial Europea a estudiar al asteroide 67P/Churyumov-Gerasimenko.                               Todas estas maniobras requieren de cambios en la velocidad y dirección del vehículo, y estos cambios se realizan a través de sus sistemas de propulsión. Para todas estas maniobras es importante el aprovechar la gravitación de los cuerpos celestes para ahorrar energía, ya que una de las limitaciones más importantes de los vehículos espaciales es la cantidad de combustible que pueden llevar desde la tierra, ya que hasta ahora no hay estaciones de reabastecimiento en el espacio.

 

El traslado de vehículos en el espacio es muy distinto a cómo estamos acostumbrados a hacerlo en la tierra. En la tierra generalmente nos movemos entre puntos que permanecen fijos entre sí. Si quiero ir de una ciudad a otra, digamos de Roma a París, las dos ciudades están fijas una con respecto a otra. En el espacio es distinto, ya que todos los cuerpos se están moviendo en órbitas todo el tiempo y las órbitas están influenciadas por la fuerza de gravedad mutua entre todos los cuerpos. El trasladar un vehículo de un cuerpo celeste a otro es parecido a lo que hace un quarterback en el futbol americano al lanzar el ovoide a un corredor. El quarterback lanza el ovoide a la posición en donde estará el corredor y no a donde está en el momento en hace el lanzamiento. Esta analogía es válida hasta cierto punto, ya que, para el caso del espacio, hay que agregar que el cuerpo celeste receptor ejercerá su propia fuerza gravitacional sobre el vehículo.

 

Así, la navegación en el espacio consiste en cambiar órbitas. Una vez que un vehículo está en una órbita, su trayectoria está determinada por la posición de los demás cuerpos celestes, por lo que si queremos cambiarla tendremos que usar combustible para cambiar la magnitud o la dirección de su velocidad. Debido a que la velocidad orbital de los vehículos espaciales es muy grande, los cambios de velocidad requeridos para maniobrar también pueden ser grandes, lo que a su vez puede requerir grandes cantidades de propelente. Y como el propelente que lleva una nave es un recurso limitado, lo tenemos que administrar de manera muy juiciosa. Por lo tanto, las maniobras espaciales deben ser muy bien planeadas y de ser posible utilizar estrategias que minimicen la cantidad de combustible empleado.

 

 

Una maniobra orbital es el cambio de órbita de un vehículo espacial a partir del empleo de un sistema de propulsión que imprime un cambio de velocidad al vehículo. Este cambio puede ser únicamente de la magnitud de la velocidad, su dirección o ambas. Las maniobras orbitales se basan en el principio de que una órbita está únicamente determinada por la posición y velocidad en un punto determinado, por lo que al cambiar la velocidad en cualquier punto, automáticamente cambiamos de órbita.
 
 
Maniobras impulsivas
 
Las maniobras impulsivas son una idealización que supone que la velocidad de una nave espacial se cambia instantáneamente, es decir en tiempo cero. En la práctica una maniobra impulsiva consiste en un breve encendido (comparado con el tiempo de recorrido de la nave espacial) de los sistemas de propulsión de la nave que permiten cambiar la magnitud, la dirección –o ambas- del vector velocidad de la nave espacial. A este cambio de velocidad se le denomina Delta v.
 
 
Existen puntos especiales en las órbitas elípticas en donde un cambio de velocidad nos conduce a otra órbita con un gasto mínimo de energía. Estos puntos son el apoapsis y el periapsis, es decir el punto más alejado y el más cercano al cuerpo central, respectivamente. Una propiedad interesante de estos puntos es que si aumentamos o disminuimos la magnitud de la velocidad precisamente al pasar por alguno de ellos, la posición del apoapsis o periapsis se mantendrá en la órbita modificada. Es decir, si por ejemplo, aumentamos la velocidad al pasar por el periapsis, la órbita modificada tendrá más energía y por lo tanto será más alargada y aumentará la velocidad en el nuevo apoapsis, pero mantendrá la posición original del periapsis.
 
Órbita de transferencia de Hohmann
En los viajes interplanetarios, es muy conveniente reducir al mínimo la masa de propelente que se necesita para realizar el viaje. De esa manera, un vuelo de este tipo es posible con las capacidades de lanzamiento actuales, y los costos no serán prohibitivos. La cantidad de propelente necesaria depende en gran medida de la ruta que se elija. Las trayectorias que por su naturaleza necesitan un mínimo de propelente son, por tanto, de gran interés.
 
En 1925, Walter Hohmann, (1880-1945) un ingeniero civil alemán interesado en los vuelos espaciales, publicó el libro Die Erreichbarkeit der Himmelskörper (La accesibilidad de los cuerpos celestes), en donde definió la órbita de transferencia de mínimo gasto de energía entre dos órbitas planetarias circulares coplanares.

 

 

 

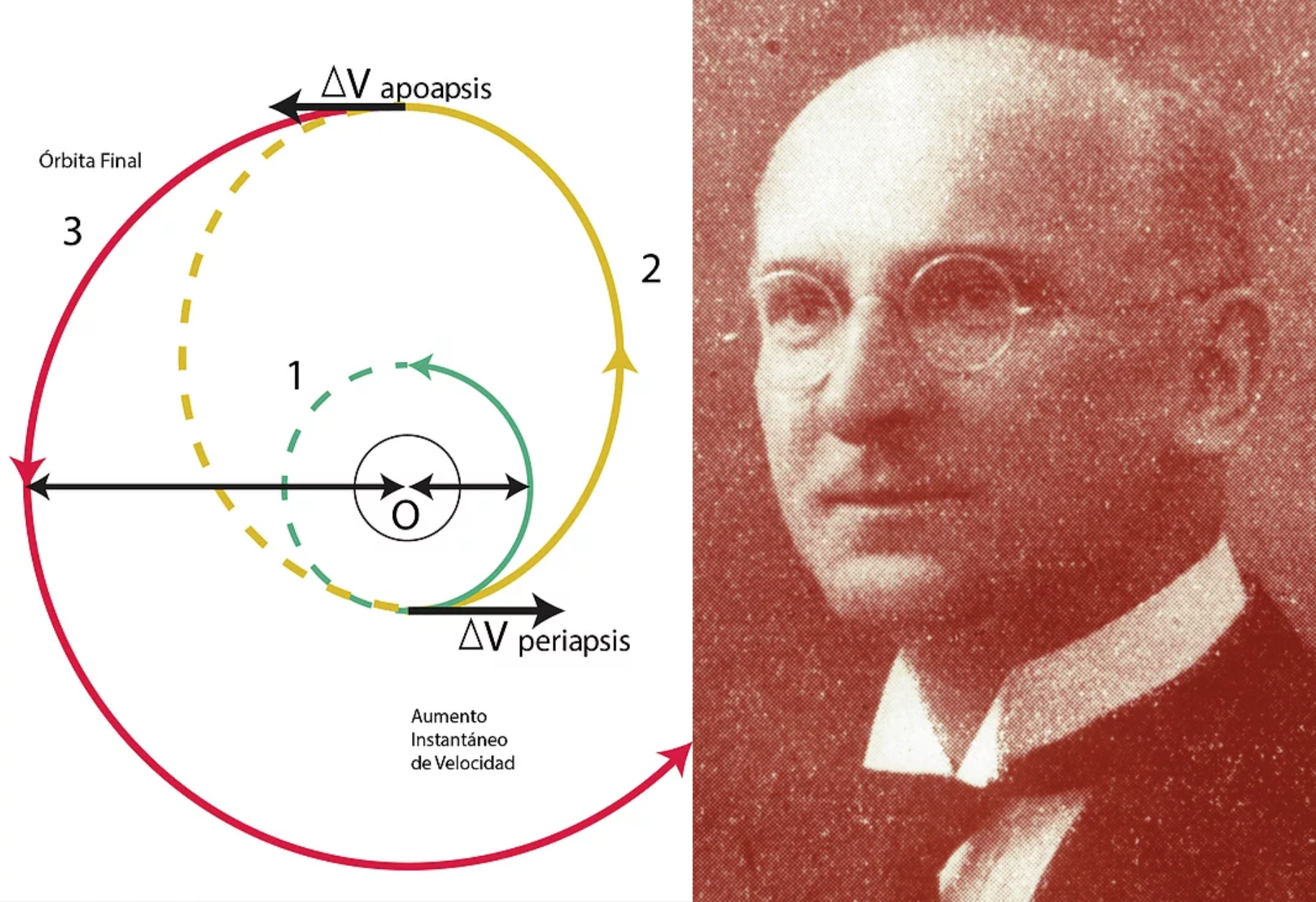
Esta órbita, llamada Órbita de Transferencia de Hohmann es una mitad de elipse que toca tangencialmente tanto la órbita inicial de partida (en verde en el diagrama) como la órbita que se quiere alcanzar (en rojo en el diagrama). La órbita de transferencia (en amarillo en el diagrama) se inicia activando el motor de la nave espacial para acelerarla y crear una órbita elíptica. Cuando la nave alcanza la órbita final, su velocidad orbital debe ser aumentada de nuevo para convertirla en una órbita circular: el motor acelera de nuevo para alcanzar la velocidad requerida. Los cambios de velocidad se supone que son instantáneos y se les conoce también como Delta-V. El Delta-V requerido en cada caso depende de los radios de las órbitas. Nótese también que la Órbita de Transferencia de Hohmann es reversible. Si se requiere pasar de la órbita de mayor radio a la de menor radio, lo que hay que hacer es frenar a la nave con sus respectivos Delta-V negativos.                                    

 

Los Delta-V respectivos en el apoapsis (el punto más lejano al cuerpo central de la órbita de transferencia) y en el periapsis (el punto más cercano) están dados por:

 

 

 

                                     

Donde mu=GM es el parámetro gravitacional, G es la constante universal de la gravitación y M es la masa del cuerpo central.

 

Para ilustrar lo anterior, veamos un ejemplo:

 

Supongamos que queremos poner en órbita geoestacionaria a un satélite que está en órbita baja ecuatorial a 300 Km de altura.

 

El radio ecuatorial de la tierra es 6,378 Km
La altura de la órbita geoestacionaria es 35,786 Km

 

Para la órbita de transferencia geoestacionaria tenemos r2 = 42,164 Km y, r1 = 6,678 Km (altitud 300 Km).

 

En la órbita baja circular, la velocidad del satélite es de 7.73 km /seg  y en la órbita geoestacionaria es 3.07 km/seg. En la órbita elíptica de transferencia la velocidad varía de 10.15 Km /seg en el perigeo a 1.61 Km/seg en el apogeo.

 

Por lo tanto, los Delta-V requeridos para poner al satélite en órbita geoestacionaria son:

 

En el perigeo: 10.15 - 7.73 = 2.42 Km/seg

 

En el apogeo: 3.07 - 1.61 = 1.46 Km/seg

 

Éstos son los incrementos en velocidad que deberán aplicarse al satélite en el perigeo y el apogeo respectivamente para colocarlo en una órbita geoestacionaria.                          

 

Como ya se mencionó, la maniobra de Hohmann requiere de la mínima cantidad de combustible para transitar entre dos órbitas circulares respecto a un cuerpo central, lo que hace que el tiempo para llevarla a cabo pueda no ser conveniente en algunos casos. Si se requiere realizar un cambio de órbita en menos tiempo, necesariamente se tendrá que aumentar el Delta-V para realizarla, tanto al inicio como al final, con el consecuente aumento en la cantidad de combustible requerido.

 

 

Aunque la Maniobra de Transferencia de Hohmann es muy útil para planear maniobras orbitales, no deja de ser una idealización, ya que las órbitas en las que se mueven las naves espaciales y los cuerpos celestes no son ni circulares ni coplanares. Por lo tanto, en los casos en los tenemos que movernos entre dos órbitas no coplanares tenemos que buscar otros procedimientos.

 

Un ejemplo de una maniobra que involucre cambios en la inclinación de una órbita es cuando queremos colocar un satélite en órbita geoestacionaria -plano de órbita en el ecuador- a partir de una órbita baja inclinada. Esto es muy común, ya que los sitios de lanzamiento no se encuentran exactamente en el ecuador -a excepción de los lanzados desde el mar por empresas como Sea Launch- por lo que las órbitas iniciales en el mejor de los casos tienen una inclinación igual a la latitud del sitio de lanzamiento.

 

En este caso tendremos que cambiar el plano de inclinación de la órbita. Una forma de lograrlo es aplicar un Delta-V en uno de los nodos orbitales, es decir uno de los puntos de intersección entre órbita inicial y la órbita deseada, con una magnitud y dirección tal que cambie el plano de inclinación de la órbita, como se aprecia en la siguiente figura.

 

 

 

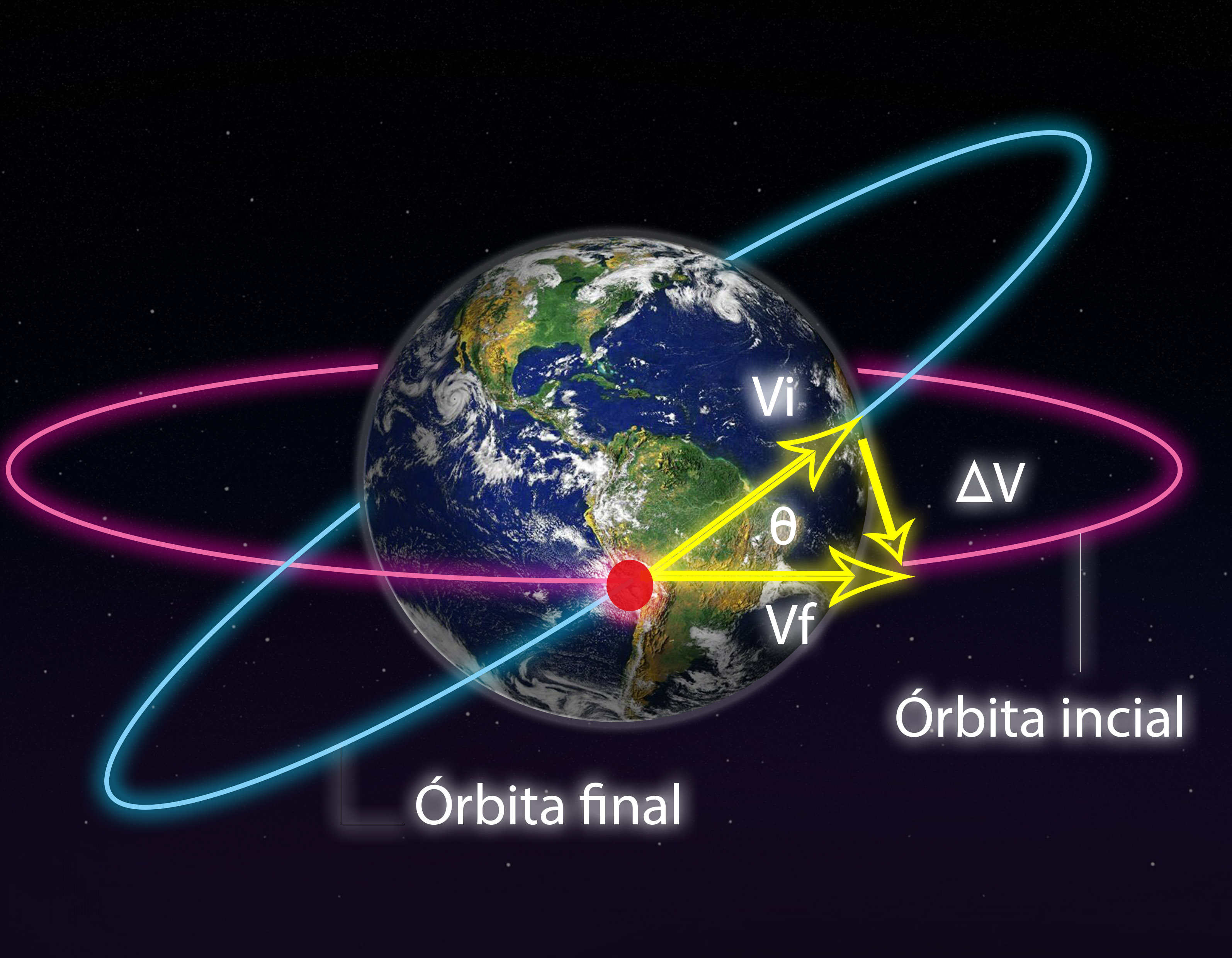
El procedimiento anterior, aunque logra cambiar la órbita, no es el más eficiente en términos de gasto de combustible. La máxima eficiencia para cambiar la inclinación de una órbita se da cuando el Delta-V se aplica en el apoapsis, en donde la velocidad orbital es mínima.

 

Hemos visto hasta aquí algunos conceptos básicos para realizar maniobras orbitales. El tema es muy extenso y fascinante y su dominio requiere de conocimientos profundos de física y matemáticas. En artículos futuros veremos algunas aplicaciones de las maniobras orbitales aplicadas a la colocación de satélites en órbitas precisas y a los viajes interplanetarios. Un excelente texto para profundizar en el tema de la Mecánica Orbital es: Orbital Mechanics for Engineering Students de Howard D. Curtis.